Stature estimation a la Bayes

---

First we are going to try to estimate the stature for one of the "Irish Giants," specifically Charles Byrne.  His stature is generally reported to have been around 7'7" (or 2310 mm).  This analysis comes from a chapter by Konigsberg and Lee Meadows Jantz in a 2018 book edited by  Latham, Bartelink, and Finnegan.

---

---

Within that Konigsberg and Jantz provided the following summary statistics for the sample with the largest sample size (N=2,015):

---

---

and the following long bone lengths for Charles Byrne:

---

---

We will use OpenBUGS to estimate the stature, but OpenBUGS is "hungry."  So first we will have to "feed" OpenBUGS some numbers from R.

---

# from: https://github.com/cran/corpcor/blob/master/R/smtools.R 

vec2sm = function(vec, diag = FALSE, order = NULL)
{
  # dimension of matrix
  n = (sqrt(1+8*length(vec))+1)/2
  if (diag == TRUE) n = n-1
  if ( ceiling(n) != floor(n) )
    stop("Length of vector incompatible with symmetric matrix")

  # fill lower triangle of matrix    
  m = matrix(NA, nrow=n, ncol=n)
  lo = lower.tri(m, diag)
  if (is.null(order))
  {
    m[lo] = vec
  }
  else
  {
    # sort vector according to order
    vec.in.order = rep(NA, length(order))
    vec.in.order[order] = vec
    m[lo] = vec.in.order
  }

  # symmetrize
  for (i in 1:(n-1))
    for (j in (i+1):n)
         m[i, j] = m[j, i]  

  return( m )
}

get.nums = function(){

N = 2015

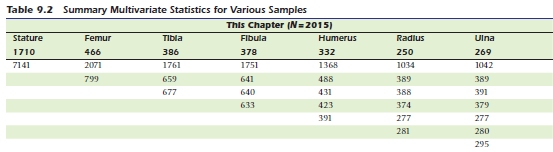
giant=c(440,329,633.5,539)

# means

mu = c(1710,332,250,466,386)
mux = mu[1]
muy = mu[-1]

# Upper triangular part of variance-covariance matrix packed as a vector

v=c(7141,2071,1761,1368,1034,799,659,488,389,677,431,388,391,277,281)

# Unpack to symmetric matrix

V=vec2sm(v,diag=T)

# Being indecisive, I changed the order of variables

V = V[c(1,4,5,2,3),c(1,4,5,2,3)]

# Partition matrix

vx = V[1,1]
vxy = V[1,-1]
Vyy = V[-1,-1]

cat('\n\n')
cat(paste('Informative prior with mean = ',round(mux,0)))
cat('\n')
cat(paste('              and precision = ',round(1/vx,5)))
cat('\n\n')

# Get regression coefficients for long bones predicted by stature

b = round(vxy/vx,7)
a = round(muy - b*mux,4)
cat('Multivariate regression coefficients: \n\n')
dput(t(rbind(a,b)))


# Inverse of conditional var/covar matrix

cat('\n\n')
cat('Inverse of residual var/covar matrix: \n\n')
dput(round(solve(Vyy-vxy%*%solve(vx)%*%t(vxy)),6))
cat('\n\n')

b=vxy%*%solve(Vyy)
a=mux-b%*%muy
stat=as.numeric(a+b%*%giant)
cat(paste('Stature estimated by multiple regression = ',round(stat,0)))
cat('\n\n')
}

get.nums()

Now we can copy the boxed text below into OpenBUGS

model
{
   # Uniform (uninformative) prior
     stat[1] ~ dunif(0,10000)
   # N(1710, 84.5) prior from reference sample, multiple regression estimate = 2159
     stat[2] ~ dnorm(1710, 0.00014)

    for(j in 1:4){
     for(i in 1:2) {Y.pred[i,j]<-theta[j] + theta[4+j] * stat[i]}}
     for(i in 1:2) {Y[i,1:4] ~ dmnorm(Y.pred[i,], tau[,])}
}

#data, note "stuttering" of long bone data
list(Y=structure(.Data=c(440,329,633.5,539,440,329,633.5,539),
.Dim=c(2,4)),theta=c(4.4156, 2.396, -29.9263, -35.693,
0.1915698, 0.1447976, 0.2900154, 0.2466041), tau =
structure(.Data= c(0.01405, -0.006103, -0.003993, 0.000363,
-0.006103, 0.019939, 0.000473, -0.00886, -0.003993, 0.000473,
0.010499, -0.005133, 0.000363, -0.00886, -0.005133,
0.011968),.Dim=c(4,4)))

Stature as an evidentiary  problem

---

First we need to "feed" OpenBUGS some new numbers:

get.nums2=function(){
N = 2015

# means

mu = c(1710,332,250,466,386)
mux = mu[1]
muy = mu[-1]

# Upper triangular part of variance-covariance matrix packed as a vector

v=c(7141,2071,1761,1368,1034,799,659,488,389,677,431,388,391,277,281)

# Unpack to symmetric matrix

V=vec2sm(v,diag=T)

# Being indecisive, I changed the order of variables

V = V[c(1,4,5,2,3),c(1,4,5,2,3)]

# Partition matrix

vx = V[1,1]
vxy = V[1,-1]
Vyy = V[-1,-1]

# Get regression coefficients for long bones predicted by stature

b = vxy/vx
a = muy - b*mux

stat=1710
v.stat=84.5^2

bones.pred = b*stat+a
cat(paste('\n\nPredicted bone lengths at stature = ',stat,'\n'))
dput(round(bones.pred,4))
cat('\n\n')

C = Vyy-vxy%*%solve(vx)%*%t(vxy)
tau = solve(b%o%b*v.stat + C)
cat('Inverse var-covar matrix of predicted bones:\n')
dput(round(tau,10))

stat=2310
v.stat=25^2

bones.pred = b*stat+a
cat(paste('\n\nPredicted bone lengths at stature = ',stat,'\n'))
dput(round(bones.pred,4))
cat('\n\n')

tau = solve(b%o%b*v.stat + C)
cat('Inverse var-covar matrix of predicted bones:\n')
dput(round(tau,10))
cat('\n\n')
}

get.nums2()

model
{
bones[1:4] ~ dmnorm(bones.pred[], tau[,])
Log.like<- -deviance(bones[1:4],bones[1:4])/2
}

#data - for N(1710, 84.5)
list(bones=c(440,329,633.5,539),bones.pred=c(332, 250, 466,
386),tau = structure(.Data= c(0.0131532986, -0.00570302,
-0.0053065435, 6.0402E-05, -0.00570302, 0.0197598473,
0.0010589323, -0.0087248683, -0.0053065435, 0.0010589323,
0.0085757009, -0.0055758772, 6.0402E-05, -0.0087248683,
-0.0055758772, 0.0118660013),.Dim=c(4,4)))

#data - for N(2310, 25)
list(bones=c(440,329,633.5,539),bones.pred=c(446.9419, 336.8786,
640.0092, 533.9625),tau = structure(.Data= c(0.0137861427,
-0.0059854557, -0.0043798194, 0.0002739931, -0.0059854557,
0.0198858971, 0.0006453392, -0.0088201931, -0.0043798194,
0.0006453392, 0.0099327771, -0.0052630986, 0.0002739931,
-0.0088201931, -0.0052630986, 0.0119380905),.Dim=c(4,4)))

formatC(exp(-14.38--33.22),format='d',big.mark=',')